Hoofdstuk 5, opgave 62
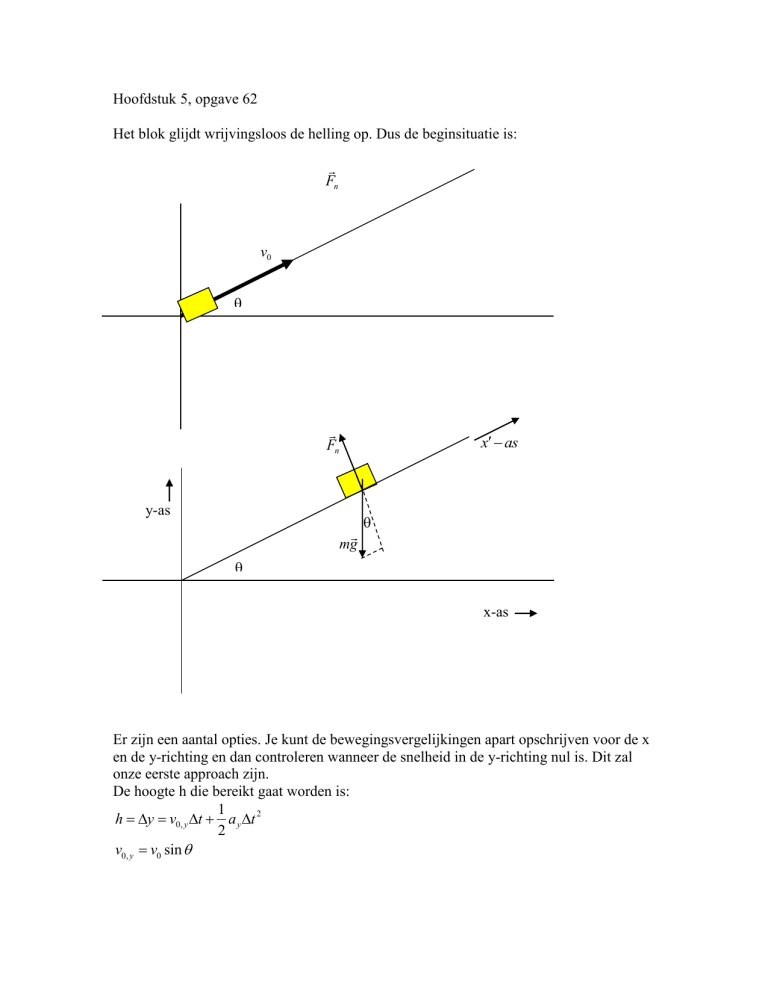
Het blok glijdt wrijvingsloos de helling op. Dus de beginsituatie is:
Fn
v0
x as
Fn
y-as
mg
x-as
Er zijn een aantal opties. Je kunt de bewegingsvergelijkingen apart opschrijven voor de x
en de y-richting en dan controleren wanneer de snelheid in de y-richting nul is. Dit zal
onze eerste approach zijn.
De hoogte h die bereikt gaat worden is:
1
h y v0, y t a y t 2
2
v0, y v0 sin
het tijdsinterval t volgt van de eis, dat op het hoogste punt de snelheid in de y-richting
v0, y
nul is: t
. Nu moeten we nog de externe kracht in de y-richting bepalen. De
ay
component van de zwaartekracht, die loodrecht op de helling staat, is gelijk aan
mg cos . Dus we hebben voor de magnitude van de normaalkracht Fn mg cos . De
sin
richting van de normaalkracht is gegeven door sin xˆ cos yˆ
. De totale
cos
externe kracht is dan gegeven door:
Fext Fn Fzw
Fext , x Fn , x mg cos sin
Fn , y mg cos 2
Fext , y Fn , y Fzw, y mg (cos 2 1) mg sin 2
cos
Fext mg sin
sin
In de laatste regel heb ik nog even uitgeschreven, dat de resulterende kracht Fext een
cos
grootte heeft van mg sin en een richting van
cos xˆ sin yˆ , dus dat is
sin
exact gelijk aan de projectie van de zwaartekracht op het oppervlak van de helling.
De versnelling in de y-richting is gelijk aan Fext , y / m g sin 2 . Hieruit volgt dat
t
v0, y
ay
v0
en de bereikte hoogte na dit tijdsinterval is
g sin
v 2 g sin 2
1
h v0, y t a y t 2 0
2
g
2
2
v0
v02
.
2g
g sin
Ook is het mogelijk om de snelheid langs de helling, dus in de x richting uit te rekenen.
Dan zou je moeten hebben gevonden dat de resulterende kracht in de x richting gelijk is
aan mg sin , dus de snelheidsvergelijking luidt: vx g sin t . De tijd om het
v0
blokje tot stilstand te laten komen bedraagt opnieuw t
. De afstand die langs
g sin
v02
1
2
de x richting wordt afgelegd is gegeven door x v0 t g sin t
. De
2
2 g sin
bereikte hoogte is deze afstand maal de sinus van de hellingshoek, dus
v2
opnieuw h sin x 0 .
2g
Een alternatieve methode is gebruik maken van de wet van behoud van energie: Als het
1
blokje tot stilstand komt is de kinetische energie afgenomen met K mv02 . Dit moet
2
gelijk zijn aan de toename in potentiele energie:
1
u mg h K mv02
2
2
v
h 0
2g












