handouts
advertisement
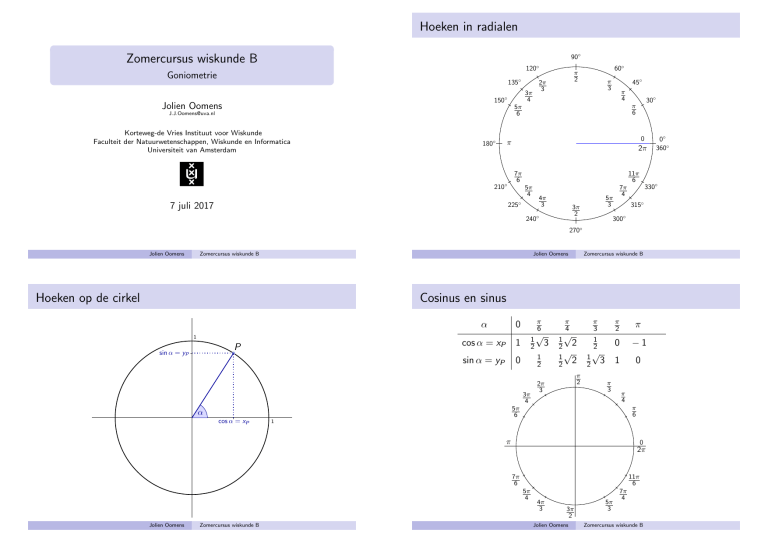
Hoeken in radialen 90◦ Zomercursus wiskunde B 120◦ Goniometrie 135◦ 2π 3 3π 4 150◦ Jolien Oomens 60◦ π 2 45◦ π 3 π 4 J.J.Oomens@uva.nl Korteweg-de Vries Instituut voor Wiskunde Faculteit der Natuurwetenschappen, Wiskunde en Informatica Universiteit van Amsterdam 180◦ 0 π 2π 7π 6 210◦ 11π 6 5π 4 4π 3 225◦ 7 juli 2017 30◦ π 6 5π 6 3π 2 240◦ 330◦ 7π 4 5π 3 315◦ 300◦ 270◦ Jolien Oomens Zomercursus wiskunde B Jolien Oomens Hoeken op de cirkel Zomercursus wiskunde B Cosinus en sinus 1 P sin α = yP π 6 0 α cos α = xP 1 sin α = yP 0 √ 1 2 1 2 3π 4 π 3 π 2 π 2 2 √ 1 2 2 1 2 0 −1 1 0 π 2 2π 3 √ 1 2 3 π 3 π 4 π 6 5π 6 α cos α = xP 3 π 4 √ 1 1 π 0 2π 7π 6 11π 6 5π 4 Jolien Oomens Zomercursus wiskunde B 4π 3 3π 2 Jolien Oomens 5π 3 0◦ 360◦ 7π 4 Zomercursus wiskunde B Rekenen met sinus en cosinus Rekenen met sinus en cosinus Bereken: Bereken: sin π = 0 π sin 2π 3 = sin 3 = cos(−π) = −1 cos 3π 2 =0 cos π6 = 1 2 √ cos 5π 4 11π sin 6 3 3π 4 α π 6 0 √ 1 cos α 1 sin α 2 π 3 2 2 √ 1 2 2 1 2 √ 1 3 1 2 0 π 4 1 2 π 3 2π 0 π 2 3π 2 -1 4π 3 5π 3 3π 2 3π 4 π 2 √ 1 2 0 π 3 π 2 1 2 2 √ 1 2 2 1 2 0 √ 3 1 2 √ 3 π π 2 π 0 2π 7π 6 7π 4 5π 3 + k · 2π met k geheel. − π2 π π 2 0 2π 3π 2 π 4 3π 4 π 2 2π 3 π 3 π 4 π 6 5π 6 0 π 0 2π 2π 7π 6 11π 6 5π 3 5π 3 3π 2 y = cos x -1 π 3π Jolien Oomens 2 4π 3 2π π 6 4π 3 11π 6 Zomercursus wiskunde B Los op: cos(x) = 12 . We vinden x = π3 + k · 2π of x = −π 5π 6 5π 4 π 6 5π 4 1 3π 2 7π 4 Zomercursus wiskunde B 7π 6 11π 6 5π 4 4π 3 π 4 1 Jolien Oomens y = sin x π 3 π 3 Vergelijkingen met cosinus en sinus -1 2π 3 1 2 π 2 2π 3 5π 6 π 4 Zomercursus wiskunde B 0 2π √ = − 12 2 11π 6 1 π 0 cos α 1 sin α π 6 1 Grafieken van de cosinus en sinus y = cos x α 0 5π 4 1 3 π − cos 7π 4 = − cos 4 − sin π6 = − 12 3π 4 π 6 7π 6 Jolien Oomens = √ π 4 π 0 3 2π 3 5π 6 π 2 √ π 2 = 1 2 3π 2 Jolien Oomens 5π 3 7π 4 Zomercursus wiskunde B 5π 2 3π 7π 4 Vergelijkingen met cosinus en sinus Goniometrische formules Gegeven 1 oplossing x0 voor cos x = u, hoe vinden we de rest? We zien dat −x0 ook een oplossing is. Alle oplossingen: x = x0 + k · 2π x = −x0 + k · 2π, of Belangrijk om te weten: 1 sin x tan x = cos x 1 = sin2 x + cos2 x k geheel. Nu sin x = u, met 1 oplossing x0 : x = x0 + k · 2π sin 2x = 2 sin x cos x x = π − x0 + k · 2π, of cos 2x = 2 cos2 x − 1 k geheel. √ Voorbeeld: sin x = 12 3. √ Met de tabel of sin−1 12 3 op oplossing x0 = π3 . Dit geeft x= π 3 + k · 2π de rekenmachine vinden we een π 3 + k · 2π = 2π 3 + k · 2π, sin α 0 √ 3 1 2 0 π 3 π 2 1 2 2 √ 1 2 2 1 2 0 √ 1 2 3 1 π 2 2π 3 3 1 2 √1 3 π 2 1 2 2 √ 1 2 2 1 2 0 √ 1 √ 1 2 √ 3 3 1 sin x 1 x − cos x Zomercursus wiskunde B π 4 π 0 2π 7π 6 11π 6 3π 2 7π 5π 4 3 π 6 0 cos α 1 1 2 1 2 √ π 4 3 1 sin α 0 2 Dus x = kπ of x met k geheel. Zomercursus wiskunde B π 2 2π 3π 3 4 α 2x = ± 31 π + k · 2π + 1 √ 2 sin(x) = 0. Dit geeft √ 2 cos(x) sin(x) − 2 sin(x) = 0 √ sin(x) 2 cos(x) − 2 = 0 √ sin(x) = 0 of 2 cos(x) − 2 = 0 1√ sin(x) = 0 of cos(x) = 2 2 π 6 Dus 2x − 1 = ± 13 π + k · 2π Jolien Oomens π 3 5π 6 5π 4 4π 3 x = ± 16 π + k · π + √ π 3 Los op: sin(2x) − π 4 √ 1 2 π 4 Ingewikkeldere opgaven 3π 4 1 2 1 1 cos x Jolien Oomens Los op: cos(2x − 1) = 12 . cos α 1 cos α π 6 Zomercursus wiskunde B Ingewikkeldere opgaven 0 0 tan α 0 Jolien Oomens α α sin α met k geheel. π 6 x = cos2 x − sin2 x. x =π− of P sin x √ π 3 1 1 2 2 2 √ √ 1 1 2 2 2 3 = ± 14 π + k · π 6 π 0 2π 1 7π 2π met k 6geheel. 5π Jolien Oomens π 4 5π 6 π 2 0 π 3 11π 6 4 4π Zomercursus wiskunde B 3 3π 2 7π 5π 4 3 Opgaven en indeling Opgaven 17.12, 17.14, 17.15, 17.31 ab, 17.32 ab, 17.33 bc en de eerste twee opgaven van het stencil. Antwoorden van de opgaven staan achterin, uitwerkingen van de extra opgaven op http://www.bliggy.net/cursusB.html. Groepen De indeling is op basis van je achternaam: A t/m D: zaal A1.14 (Gideon Jager) E t/m Kuhl: zaal A1.30 (Jeroen Eijkens) Kuhlhan t/m Seydel: zaal D1.114 (Sebastian Zur) Simsir t/m Z: zaal D1.116 (Thijs Benjamins) Jolien Oomens Zomercursus wiskunde B